Background

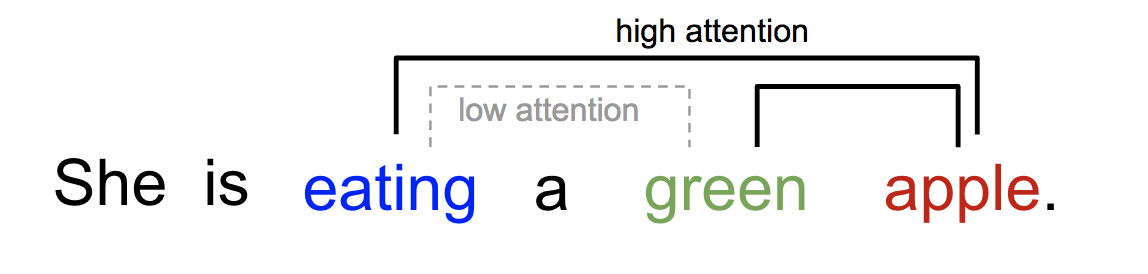
Self-attention, it is a mechanism first used for nature language processing, such as language translation and text content summary,etc. Self-attention sometimes called intra-attention is an attention mechanism relating different positions of a single sequence in order to compute a representation of the sequence, the sequence can be a phrase in NPL task. At the time Google Brain released ^[1]“Attention is all you need.”, this mechanism have already become an integral part of compelling sequence modeling and transduction models in various tasks. However such attention mechanism are used in conjunction with a recurrent network(RNN) or a convolutonal network(CNN). Given a sequence of words, if we see the word “eating”, then we will take more attention to the following name of food.

Seq2seq

One of the example of the application of this mechanism is the famous ^[2]“Sequence to Sequence Learning with Neural Networks” model. Broadly speaking, it aims to transform an input sequence (source) to a new one (target) and both sequences can be of arbitrary lengths. Examples of transformation tasks include machine translation between multiple languages in either text or audio, and for tasks like adding video caption is also possible. The main struture Seq2seq model uses is the Encoder-Decoder structure.

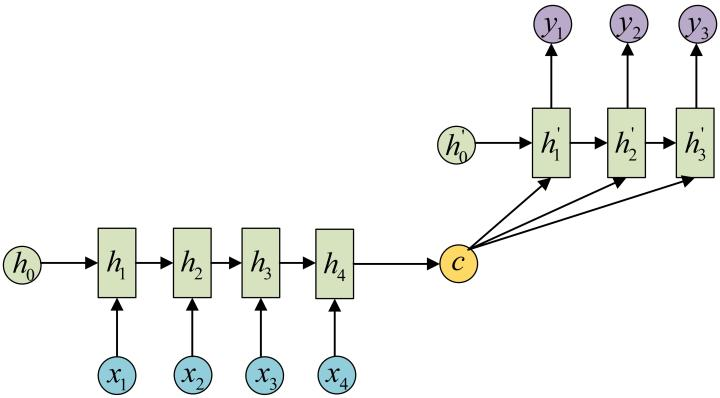
• Encoder processes the input sequence and compresses the information into a context vector of a fixed length. This vector is expected to be the encoded information or meaning of the input sequence.
• Decoder is initialized with the context vector to emit the transformed output. The early work only used the last state of the encoder network as the decoder initial state.
  Both the encoder and decoder are recurrent neural networks, i.e. using LSTM or GRU units.

disadvantages While, there are some disadvantages of RNN for this task. Fixed-length context vector design is incapability of remembering long sentences. And for RNN, it has forgetten the fisrt parts once it completes processing the whole input. It also hard to parallel the whole processes, as the layers is run in sequence.

CNN

People try to use CNN to solve the parallel issue.
^[3]“Transformer”

But we have to build a lot more filter to have large receptive field.

Transformer

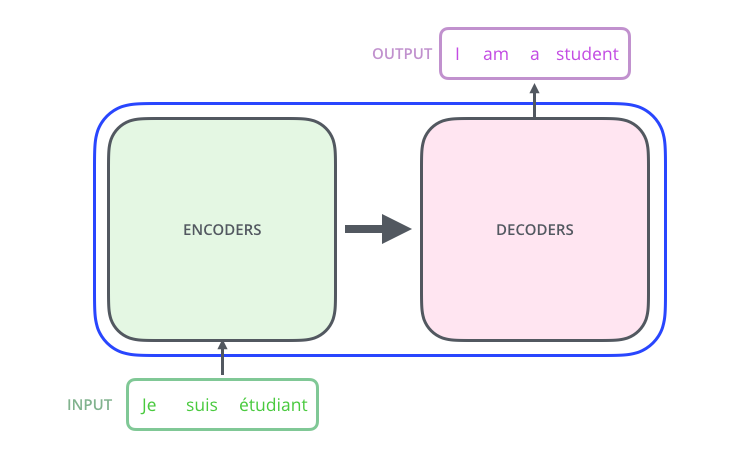
The Transformer is a model proposed in ^[1] based entirely on attention and almost all tasks use a RNN to perform attention mechanism can be repaced by the Transformer. The transformer as the new stat-of-art in 2020 outperforms the Google’s Neural Machine Translation System ^[5]“GNMT” in specific tasks. The biggest benefit, however, comes from how The Transformer lends itself to parallelization. It is in fact Google Cloud’s recommendation to use The Transformer as a reference model to use their Cloud TPU offering.

Model Architecture

The Transformer also take the encode-decoder structure. A high level structure is showed below:
^[6]“The Illustrated Transformer”

The encoder maps an input sequence of sybol representations $x = (x_1,..,x_3)$ to a sequence of continous representations $z = (z_1,…,z_n)$. Given $z$, the decoder then generate an output sequence $y = (y_1,…,y_3)$ of symbols one element at a time. At each step the model is auto-regressive, consuming the previously generated symbols as additional input when generating the next. This will be represented in masking process in the decoder.

While a more detailed model architecture is represented in “Attention is all you need”^[1] as below:

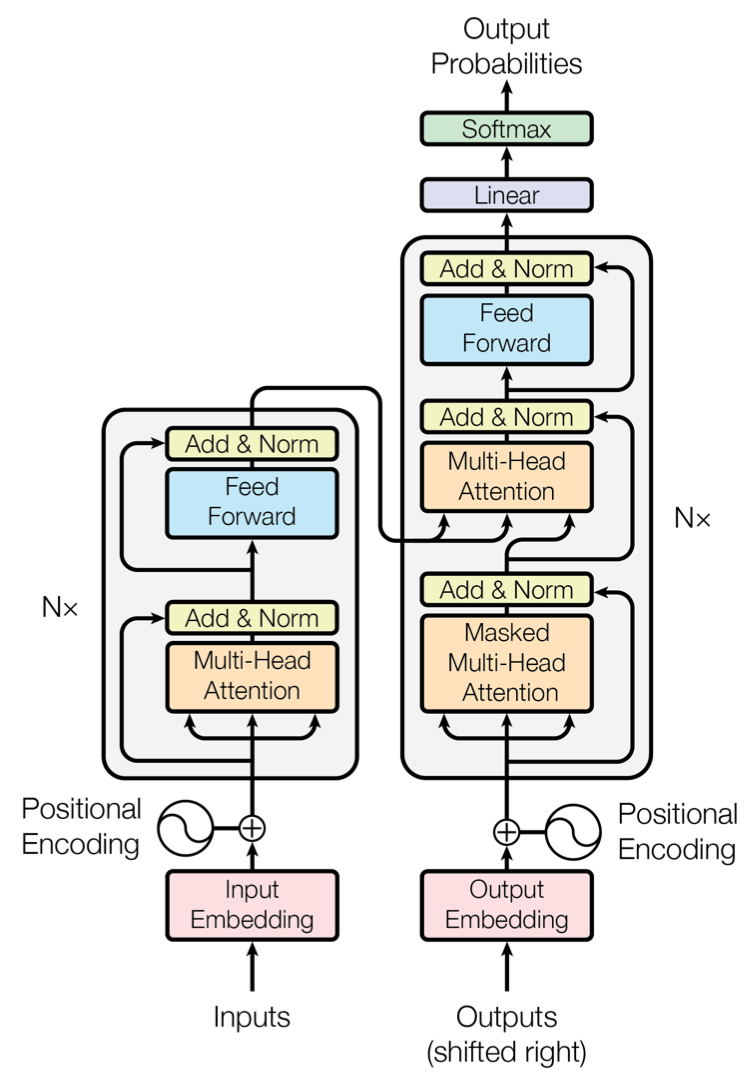
• The Encoder is composed of a tack of N=6 identical layers. For each layer, it has:

  1. A multi-head self-attention mechanism sub-layer.
  2. A position-wise fully connected feed-forward network sub-layer.

• The Decoder is also composed of a stack of N=6 identical layers. For each layer, it has:

  1. A multi-head self-attention mechanism sub-layer. The masking proceess I talk about before is added here too. Combined with fact that the output embeddings are offset by one position, ensure that the predictions for position $i$ can depend only on the known outputs at positions less than i.
  2. A new multi-head self-attention machanism sub-layer, which performs attention over the output of the encoder stack.
  3. A position-wise fully connected feed-forward network sub-layer.

For each sub-layer, it has two operations:

• A residual connection, like in ^[7]“Deep Residual Learning for Image Recognition”.
• A layer normalisation^[8]“Layer Normalization”

The output of each sub-layer is LayerNorm(x + Sublayer(x)), where Sublayer(x) is the function implemented by the sub-layer itself.

To facilitate the residual connections, all sub-layers in the model, as well as the embedding layers, produce outputs of dimension $d_{model}=512$

A detail analyse of decoder

How does each step work

I was confused in the concept of a masking process showed in the first sub-layer in the decoder and how does the model is auto-regressive at each step. Let’s have a further look at the functionality of the decoder.

After finishing the encoding phase, the decoding phase begins. Each step in the decoding phase outputs an element from the output sequence. The number of steps depends on a special symbol which is generated and indicate that the decoder has completed its output.

At the begining, a defaut parameter element which indicate the begin of the output sequence is generate from the output of the encoder and then for each step, the elements from the previous generated sequence will be fed into the decoder and that is why we need a mask to let decoder to see only the output at position less than $i$ which is the indice of step (prediction for position $i$). After the fisrt self-attention layer, the output of this layer will meet the hidden elements generated from the encoder(I will explain these hidden element later in the attention function) and go through the whole decoder stack. The mask process is done by masking future positions (setting them to -inf) before the softmax step in the self-attention calculation.
^[6]“The Illustrated Transformer”

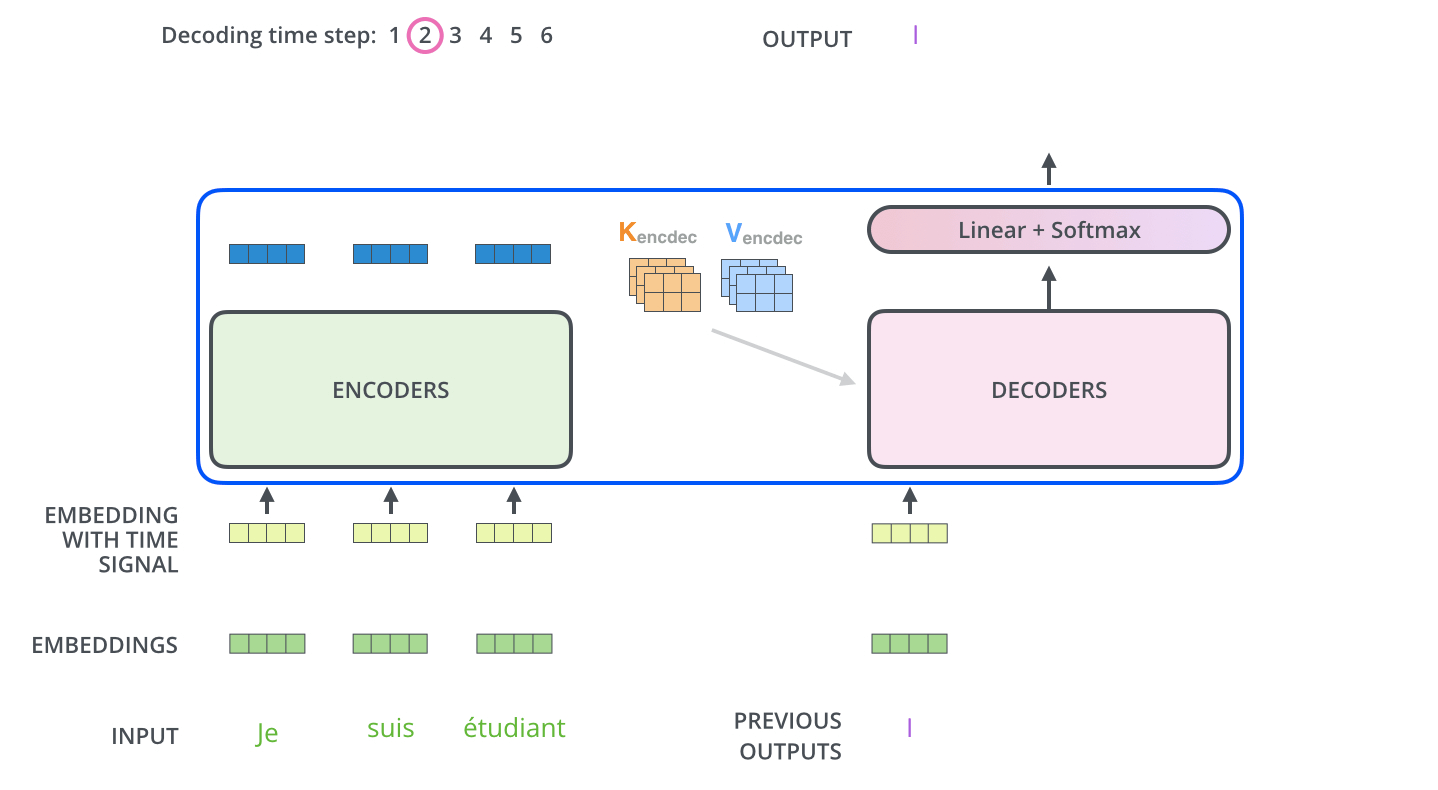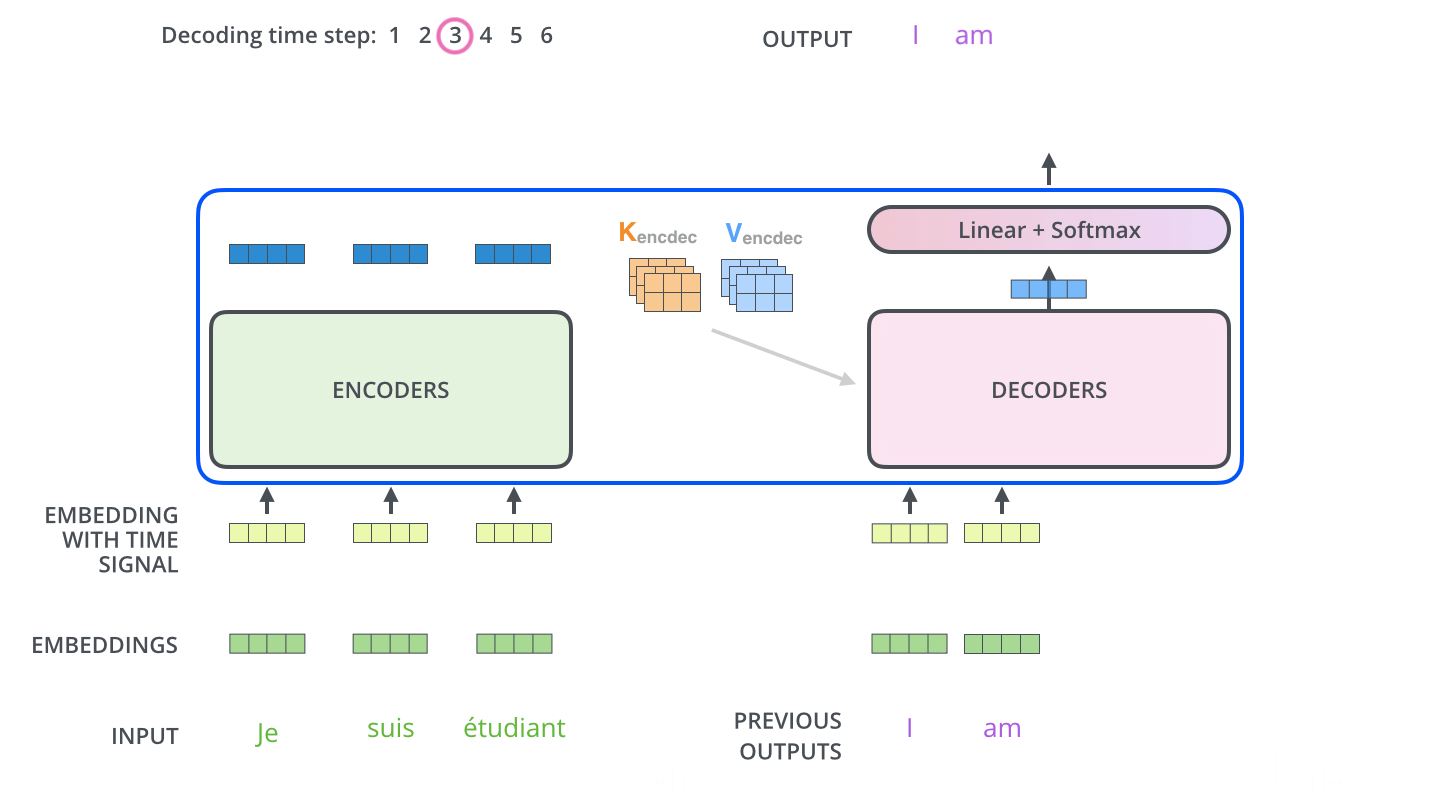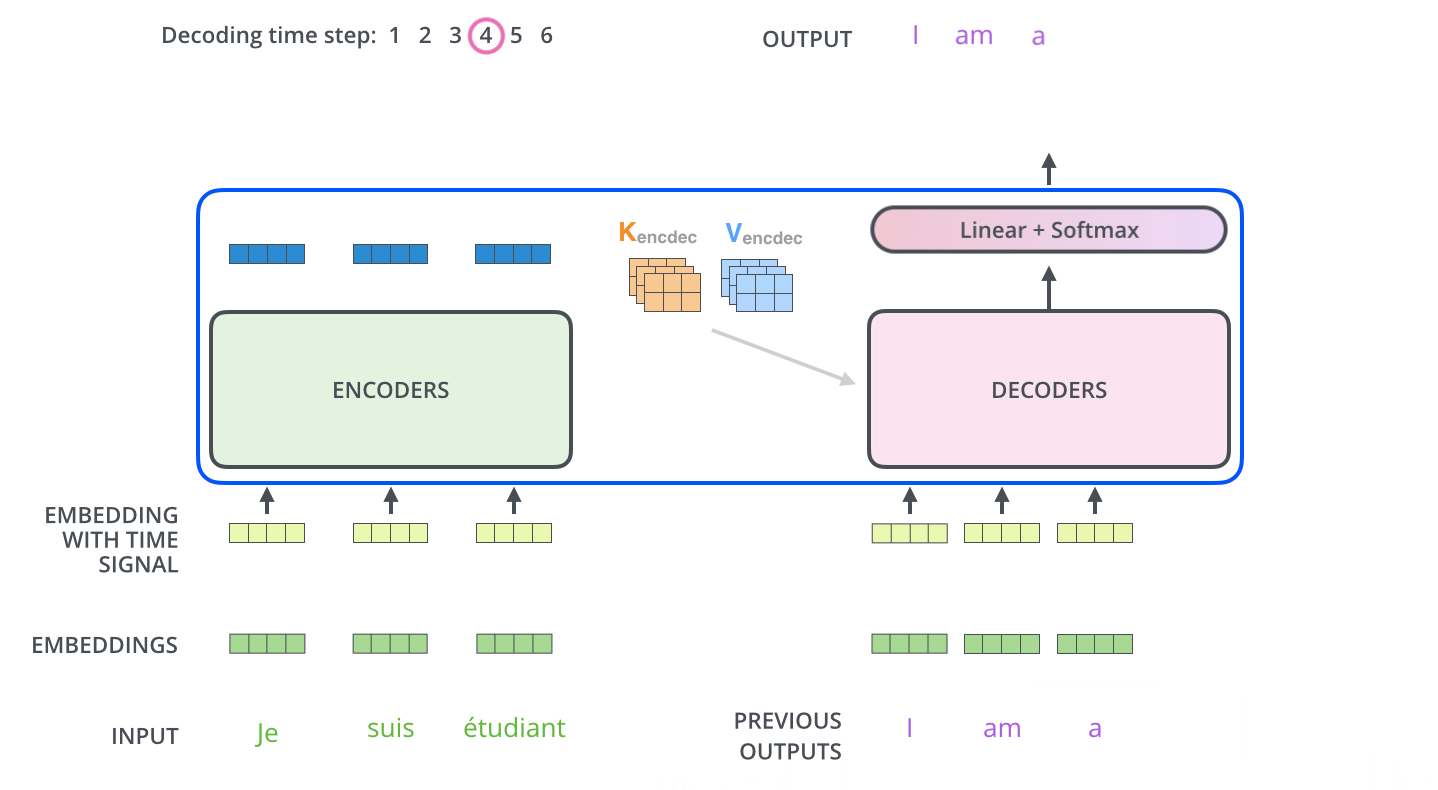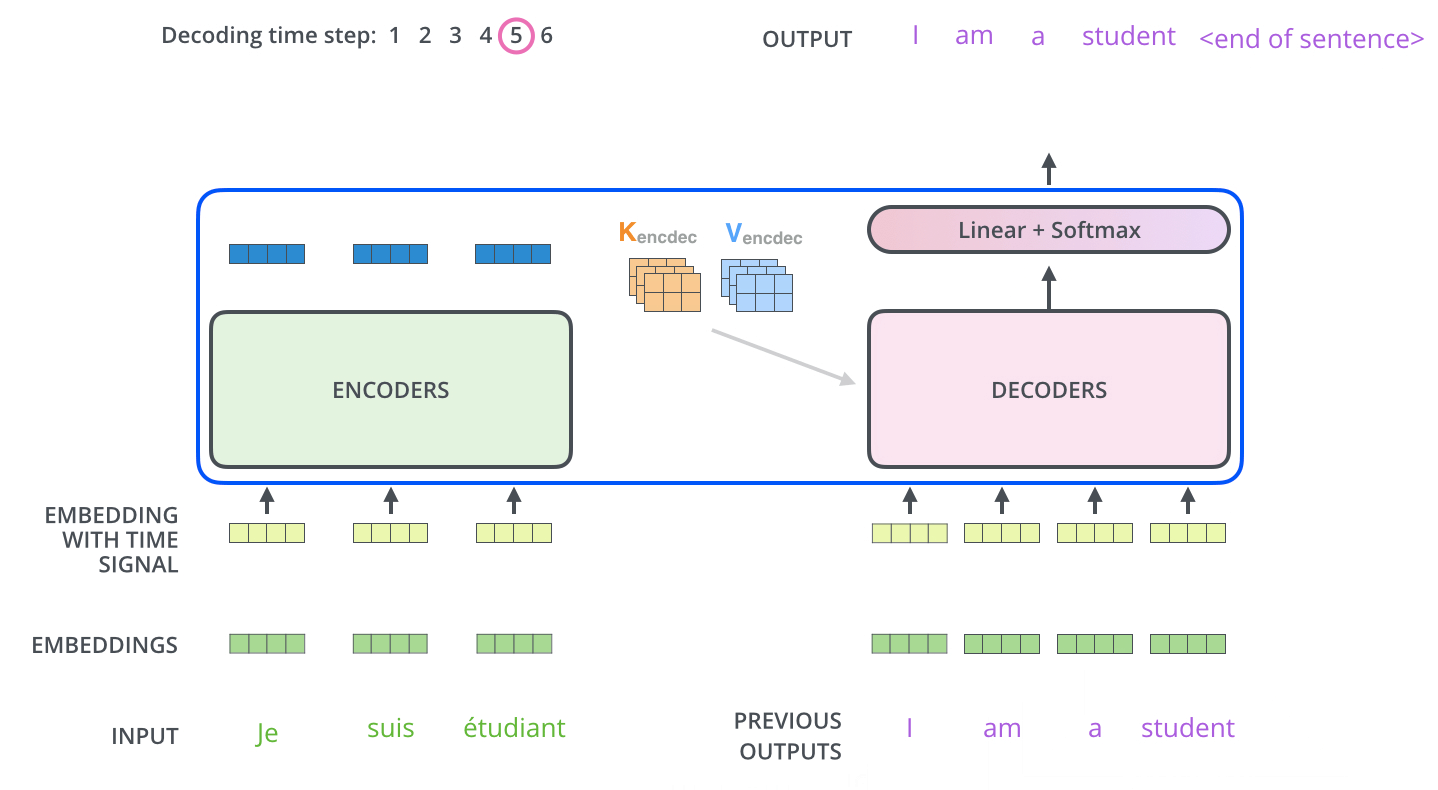
“Illustrated Guide to Transformers- Step by Step Explanation”

Final linear layer and Softmax layer

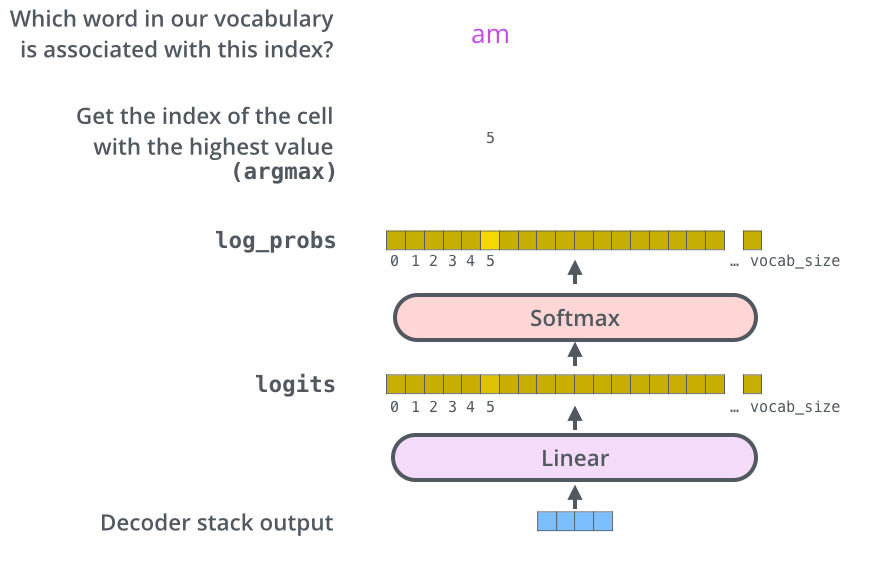
The decoder stack outputs a vector of floats and it is final linear layer and softmax layer to turn them into the sequence of worlds.

For example, the model knows 10,000 unique English world from its training dataset. The linear layer is then a simple fully connected neural network that takes input as decoder stack’s outputs vector and output a 10,000 dimension vector. The softmax layer turns the values in this vector into probabilities (all positive, all add up to 1.0). The cell with the highest probability is chosen, and the word associated with it is produced as the output for this time step.
^[6]“The Illustrated Transformer”

For the training process, given the vectors of probabilities for the whole predicted sequence, we can then do the backpropagation for the whole model including the encoder and the decoder.

Attention

In the context of neural networks, attention is a technique that mimics cognitive attention. The effect enhances the important parts of the input data and fades out the rest – the thought being that the network should devote more computing power on that small but important part of the data. Which part of the data is more important than others depends on the context and is learned through training data by gradient descent.

The Transformer has it’s own attention mechanism called “Scaled Dot-Product Attention”. I’m going to introduce this model in the following

Query, Key, Value

The basic elements of this model is k: query, k: key of dimension $d_k$ and v: value of dimension $d_v$.
The matrix of attention is showed below:
^[1]“Attention is all you need”
$$
Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V
$$
where, the compute attention function on a set of queries simultaneously, packed together into a matrix Q. The keys and values are also packed together into matrices K and V. Let’s just keep this equation in mind for now.

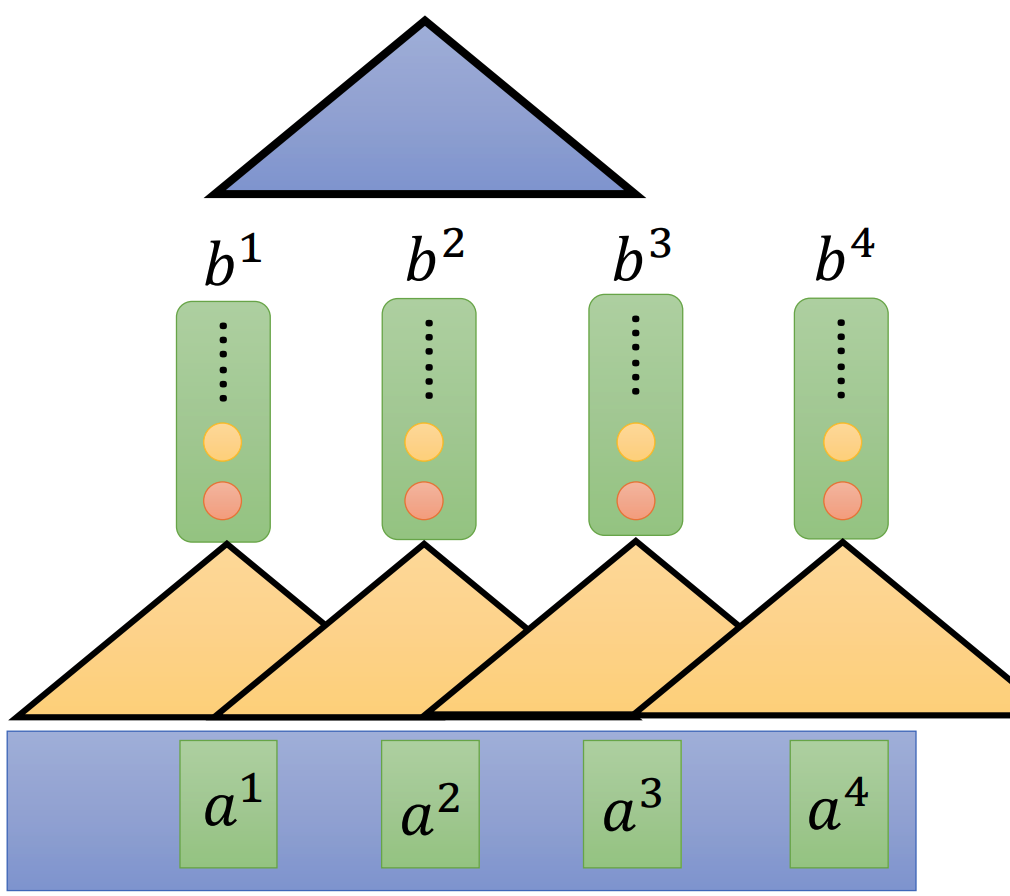
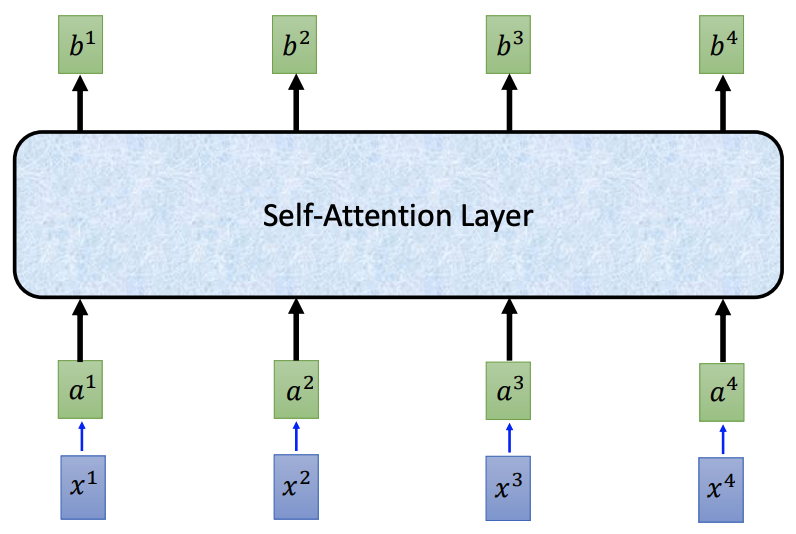
The high level view of self-attention Layer is like this:
^[3]“Transformer”

Let’s have a deeper view of “Scaled Dot-Product Attention”.

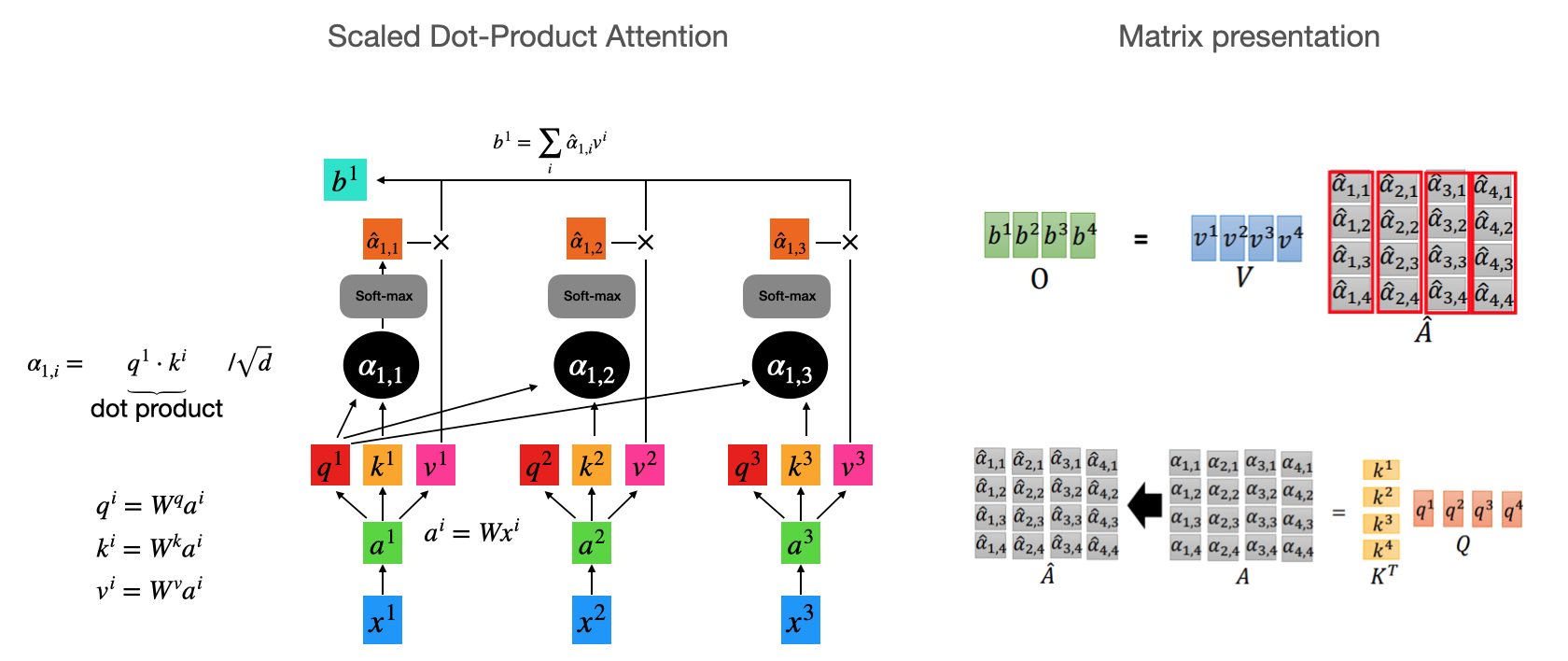
This is the schema to compute the scaled Dot-Product attention given an input sequence. People also often use additive attention that compute the compatibility function using a feed-forward network with a single hidden layer. While dot-product attention is much faster and more space-efficient in pratice. But the dot products grow large in magnitude. Assume that the components of $q$ and $k$ are independant random variable with mean 0 and vriance 1. Then their dot product, $q \cdot k = \sum^{d_k}_{i=1}$, has mean 0 and variance $d_k$. So we have the term $\sqrt{d_k}$ to scale the dot product.

Multi-head Attention

From the paper of the Transformer, they found that it benecial to linearly project the queries, keys, and values h times with different, learned linear projections to $d_k$, $d_k$ and $d_v$ dimensions, respectively. It generate h $d_v$-dimensional output values in parallel and these are concatenated and once again projected, resulting in the final values.
$$
MultiHead(Q, K, V) = Concat(head_1, …, head_h)W^o
$$
where
$$
\text{head}_{i} = \text{Attention}(QW^{Q}_{i}, KW^{K}_{i}, VW^{V}_{i})
$$

Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.

^[3]“Transformer”

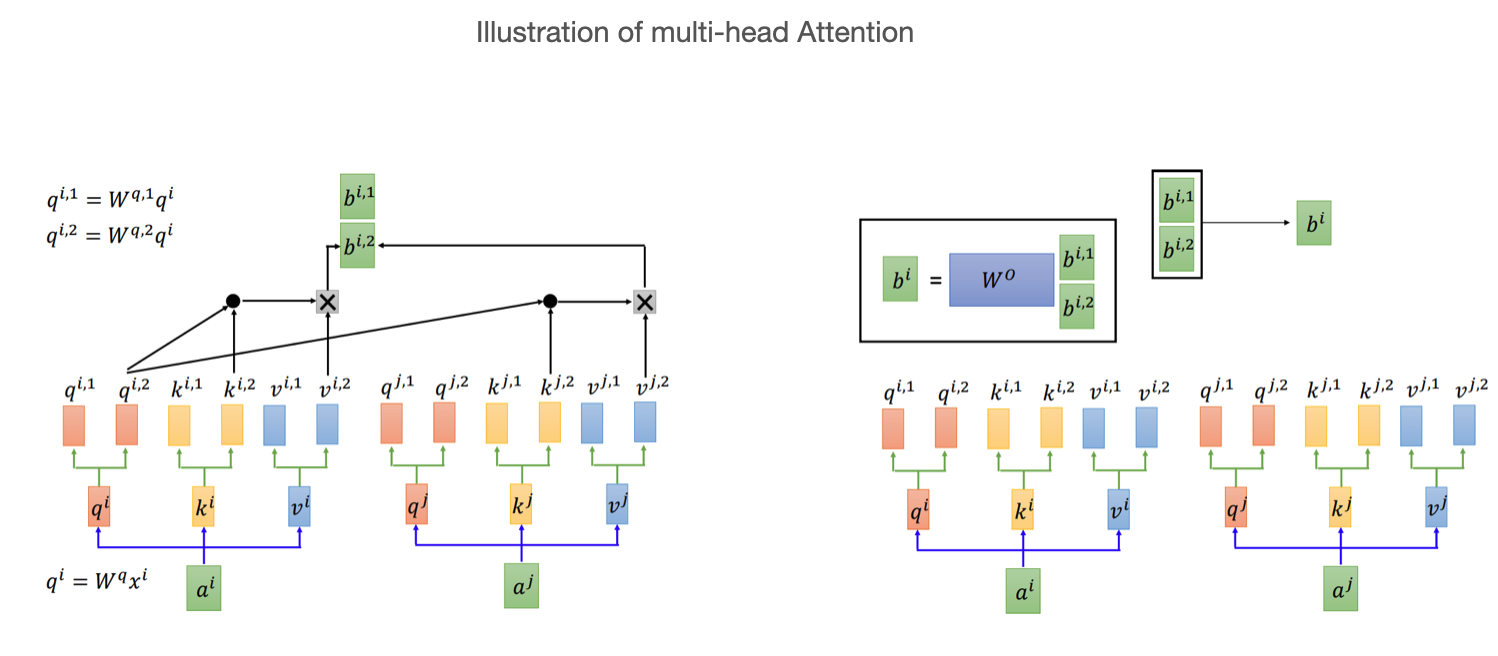
Other main parts

From the Transformer model architecture schema, we can notice that there are also several other components and I am going to do an introduction to these parts this section.

Position-wise Feed-Forward Networks

Position-wise Feed-Forward Networks is named Feed Forward in the model architecture schema and it is included in each layer of encoder and decoder. It is consists of two linear transformations with a RELU activation in between.
$$
FFN(x) = RELU(xW_1 + b_1)W_2 + b_2
$$
This function is applied to each position separately and identically, another way of describing this is as two convolutions with kernal size 1. While the linear transfermations are the same across different positions,they use different parameters from layer to layer(different $W$ and $b$).

Embeddings

Embeddings are learned to convert the input tokens and output tokens to vectors of dimension $d_{model}$. Two embedding layer in encoder, decoder and the pre-softmax linear transformation at the output of the final decoder stack share the same weight matrix. They also multiply those weights by $\sqrt{d_{model}}$

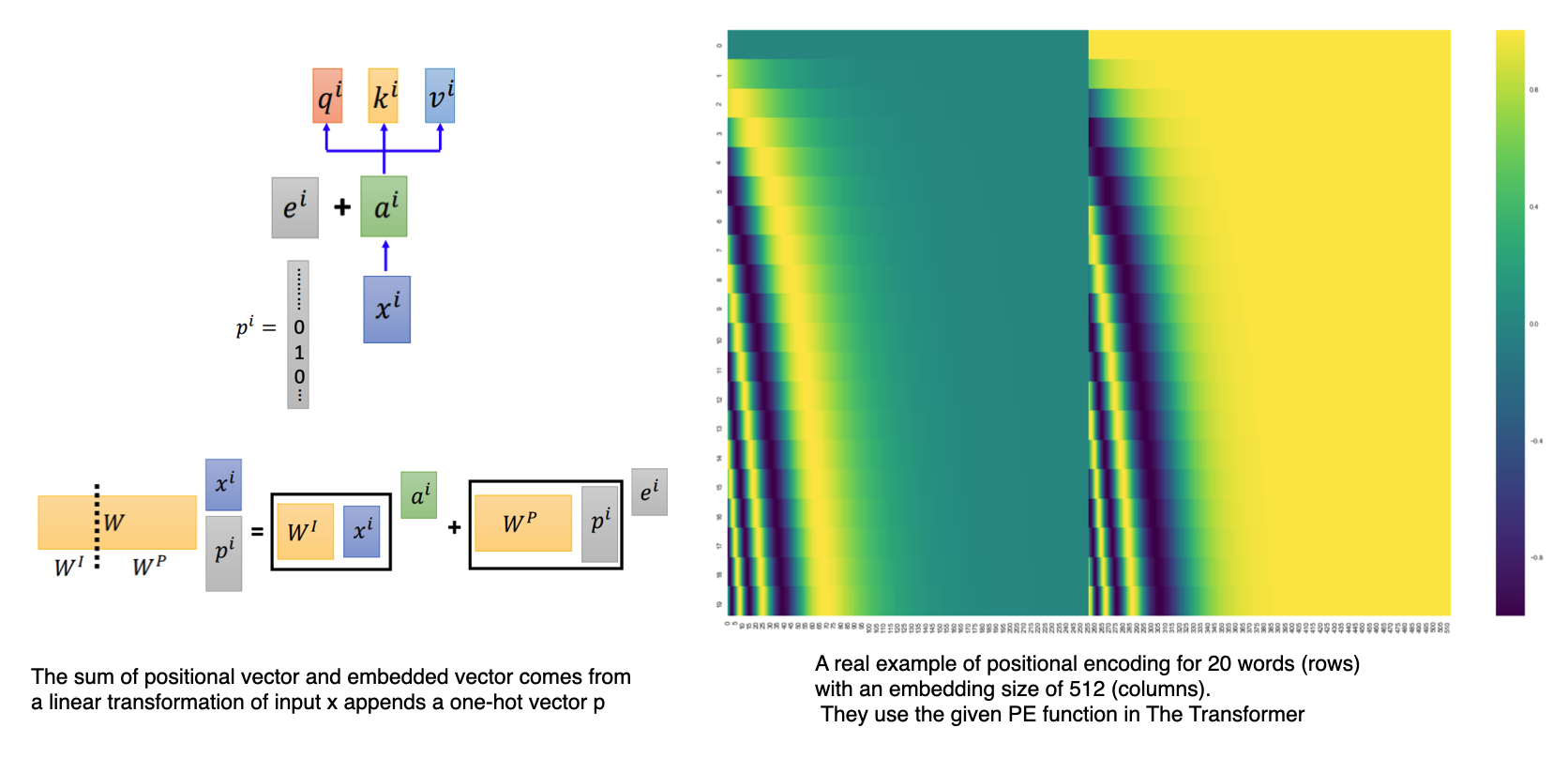
Positional Encoding

We can notice that there is no positional information in self-attention as it is composed of dot product operations in parallel for each element of different position in the sequence. Some information about the relative or absolute position of the tokens in sequence need to be injected. The authors of The Transformer^[3] add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks.The positional encoding have the same dimension $d_{model}$ as the embeddings, so that the two can be summed. While, there are many other choices of positional encodings, learned and fixed.

An intuitive way to understand the sum operation between vector of position encoding and the vector of embedded input showed below.
^[3]“Transformer”
^[6]“The Illustrated Transformer”

By summing these two terms, we integrate the one-hot vector which contains the current position information into the input.

Why Transformer is good

The reasons why Transformer becomes the stat-of-art in 2017 and has appealed attention in AI recently is listed below:

1. The relative low computational complexity per layer.
2. The large amount of computation that can be parallelized.
3. The path length between long-range dependencies in the networl. As we can see that during the generation of Attention, an input element need to dot product with all other inputs and than generate weights and finally gets its attention element by the weighted average on the value of other input elements. It keeps the local and global information.

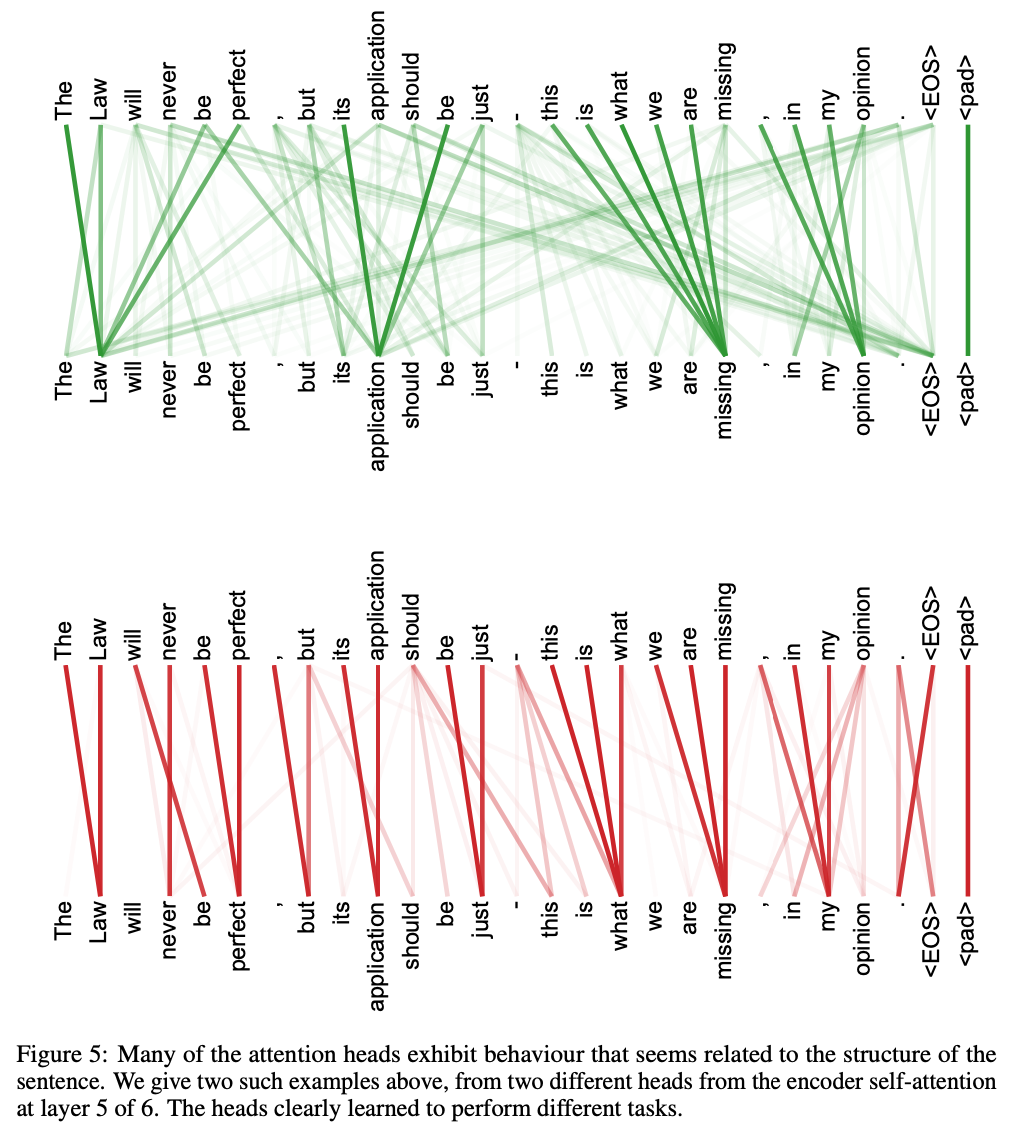
Some interesting images from the paper

^[1]“Attention is all you need”

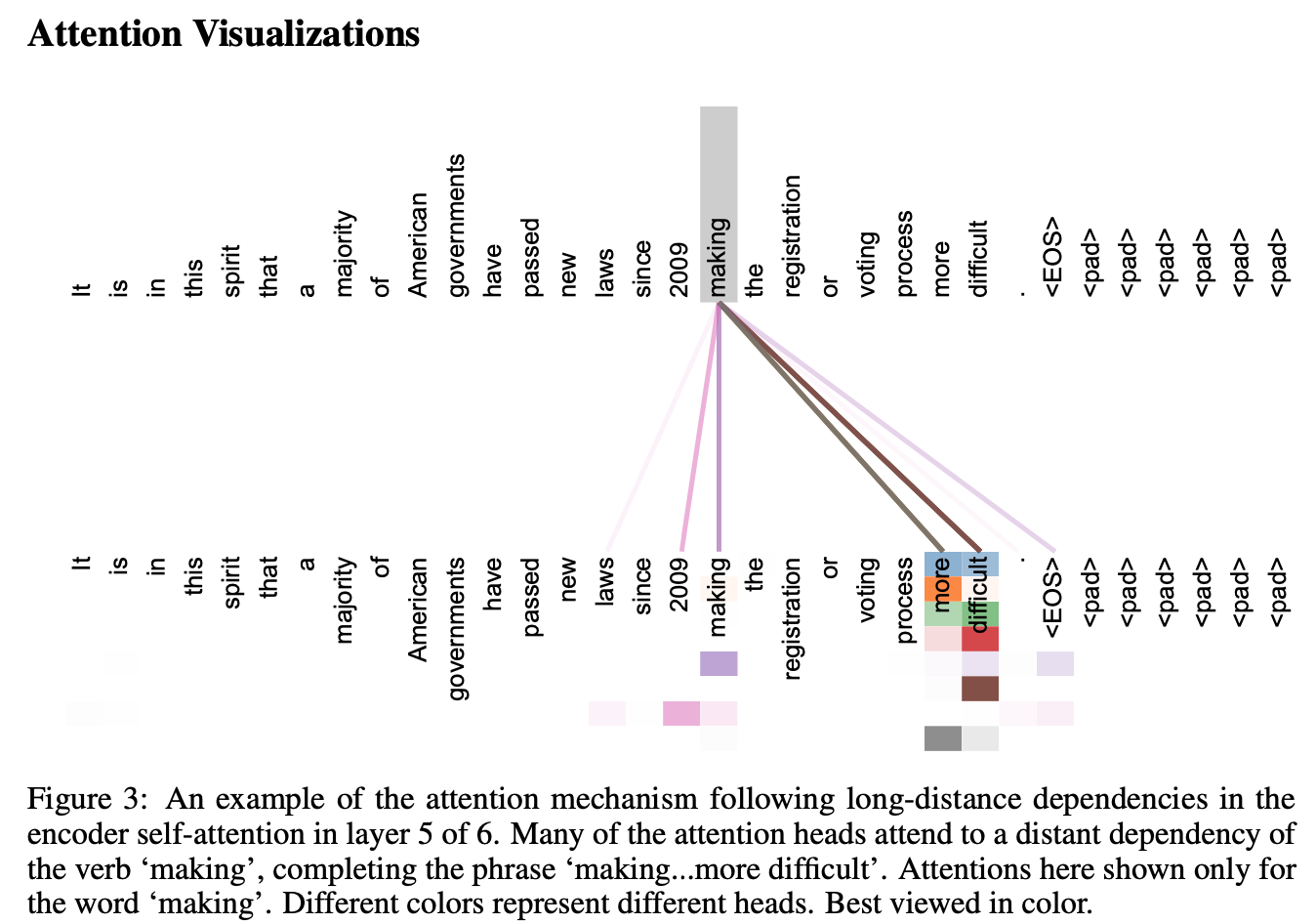
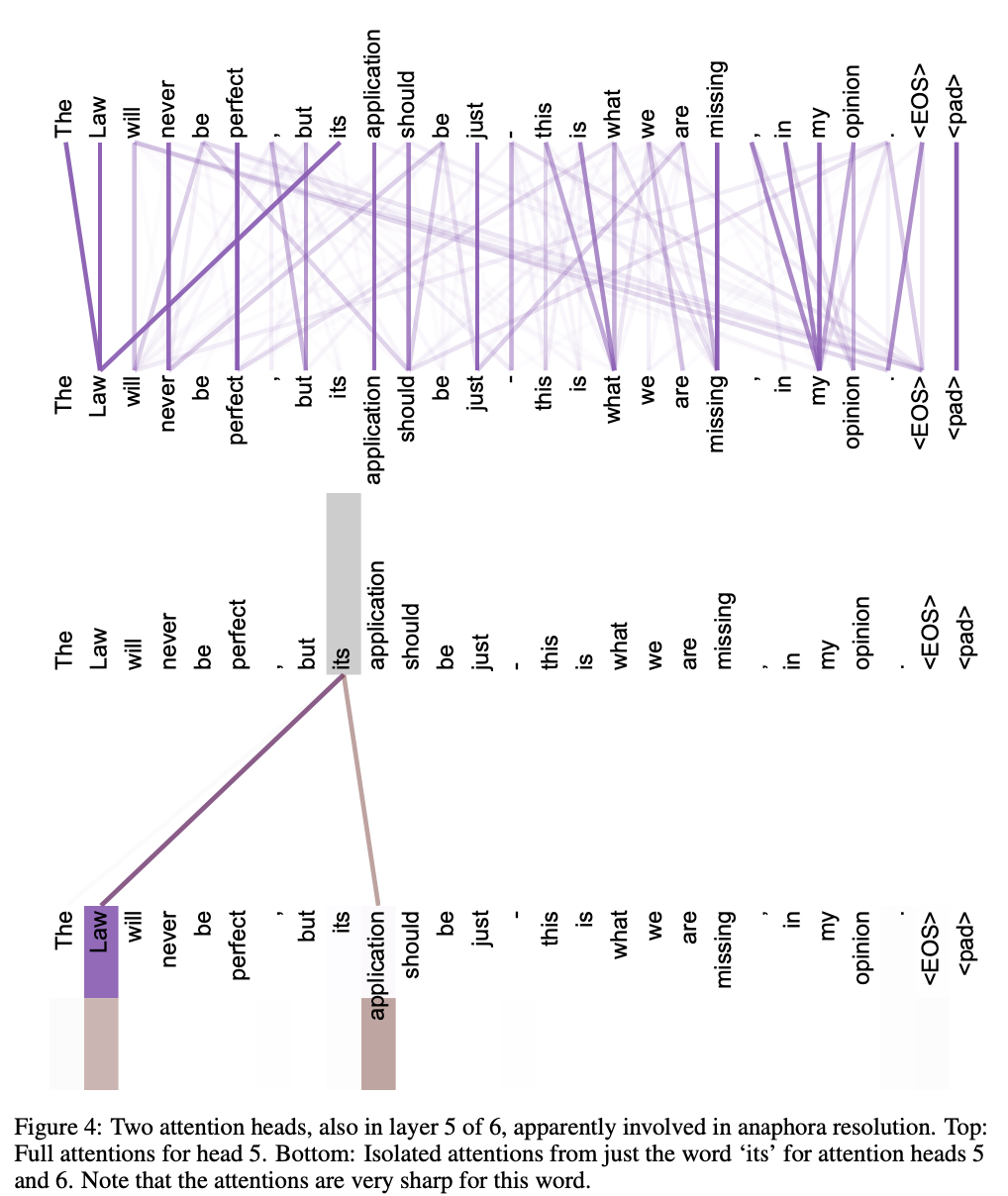
Citation

@article{zhao_Attention2021, 
    title={Transformer? Attention!}, 
    url={https://blog.yunfeizhao.com/2021/03/31/attention/}, 
    journal={https://blog.yunfeizhao.com/}, 
    author={ZHAO, Yunfei}, year={2021}, month={Mar}}

References

1. Ashish Vaswani, et al. “Attention is all you need” NIPS 2017. ↩
2. Ilya Sutskever, et al. “Sequence to Sequence Learning with Neural Networks”NIPS 2014. ↩
3. Hung-yi Lee. “Transformer” ↩
4. Nicolas Carion, Francisco Massa et al. “End-to-End Object Detection with Transformers”ECCV 2020. ↩
5. Yonghui Wu et al. “Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation”CoRR 2016 ↩
6. Jay Alammar“The Illustrated Transformer” ↩
7. K. He, X. Zhang, S. Ren and J. Sun “Deep Residual Learning for Image Recognition,” 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016, pp. 770-778, doi: 10.1109/CVPR.2016.90. ↩
8. Jimmy Lei Ba et al. “Layer Normalization” ↩
9. Michael Phi “Illustrated Guide to Transformers- Step by Step Explanation” ↩