Multimodal Sentiment Analysis (MSA) is a growing field that combines various data modalities to analyze and interpret human emotions. Intrinsically human comminication is multimodal (heterogeneous), temporal and asynchronous and it consists of the language (words), visual (expressions), and acoustic (paralinguistic) modalities all in the form of asynchronous coordinated sequences.
This project focuses on the challenge of multimodal sentiment analysis (MSA). The goal is to develop models that can effectively classify sentiment with explanability across language (words), visual (expressions), and acoustic (paralinguistic) modalities. Here are some useful links:
The main idea is to create a system that can understand and explain the sentiment expressed in a given video and classify it into the following categories:
- SNEC: strong negative emotion
- WNEG: weak negative emotion
- NEUT: neutral emotion
- WPOS: weak positive emotion
- SPOS: strong positive emotion
There are also other ways to classify the sentiment, such as using the valence-arousal-dominance (VAD) model, which is a continuous representation of emotion. The VAD model classifies emotions based on three dimensions: valence (pleasantness), arousal (activation), and dominance (control).
| Emotion | Valence | Activation | Dominance |
|---|---|---|---|
| Joy | High | High | High |
| Anger | Low | High | High |
| Fear | Low | High | Low |
| Boredom | Low | Low | Low |
| Calm | High | Low | High |
So in this challenge, we consider only the Valence and we may use the other dimensions for the prediction of Valence.
Dataset
Two public multimodal datasets are used for this challenge:
CMU-MOSEI
The original parpar is “Multimodal Language Analysis in the Wild CMU-MOSEI Dataset and Interpretable Dynamic Fusion Graph”. It is published in 2018 by Zadeh et al. The CMU-MOSEI dataset is a large-scale multimodal sentiment analysis dataset that includes videos, audio, and text data. It is designed to facilitate research in multimodal sentiment analysis and emotion recognition.
CMU-MOSEI contains 23,453 annotated video segments from 1,000 distinct speakers and 250 topics. Each video segment contains manual transcription aligned with audio to phoneme level. All the videos are gathered from online video sharing websites.
It ensures the diversity in the training samples (intra-modal and cross-modal dynamics for language), variety in the topics, diversity of speakers, and variety in annotations. A segment is annotated for the presence of 9 emotions (angry, excited, fear, sad, surprised, frustrated, happy, disappointed and neutral) as well as valence, arousal and dominance.
This paper studied how the fusion is performed in terms of what modalities are related and how modalities engage in an interaction during fusion. The paper also proposed a new fusion method called Dynamic Fusion Graph (DFG) that can dynamically fuse the modalities based on their relevance and interaction. And a model called Graph Memory Fusion Network (Graph-MFN) is built on top of DFG and Memory Fusion Network (MFN).
Feature Extraction
Language: GloVe (Global Vectors for Word Representation) word embeddings (Pennington et al., 2014) were used to extract word vectors from transcripts.
Visual: Frames are extracted from the full videos at 30Hz. The bounding box of the face is extracted using the MTCNN face detection algorithm (Zhang et al., 2016). We extract facial action units through Facial Action Coding System (FACS) (Ekman et al., 1980).They also extract a set of six basic emotions purely from static faces using Emotient FACET (iMotions, 2017). MultiComp OpenFace (Baltruˇ saitis et al., 2016) is used to extract the set of 68 facial landmarks, 20 facial shape parameters, facial HoG features, head pose, head orientation and eye gaze (Baltrusaitis et al., 2016). Finally, we extract face embeddings from commonly used facial recognition models such as DeepFace (Taigman et al., 2014), FaceNet (Schroff et al., 2015) and SphereFace (Liu et al., 2017).
Acoustic: They use the COVAREP software (Degottex et al., 2014) to extract acoustic features including 12 Mel-frequency cepstral coefficients, pitch, voiced/unvoiced segmenting features (Drugman and Alwan, 2011), glottal source parameters (Drugman et al., 2012; Alku et al., 1997, 2002), peak slope parameters and maxima dispersion quotients (Kane and Gobl, 2013). All extracted features are related to emotions and tone of speech.
CH-SIMS v2.0
This dataset is proposed in the paper “Make Acoustic and Visual Cues Matter: CH-SIMS v2.0 Dataset and AV-Mixup Consistent Module”
In the paper they emphasize making non-verbal cues matter for the MSA task. CH-SIMS v2.0 doubles CH-SIMS size with another 2121 refined video segments. From the model perspective, benefiting from the unimodal annotations and the unsupervised data in the CH-SIMS v2.0, the Acoustic Visual Mixup Consistent (AV-MC) framework is proposed.
State of the art
The state of the art in MSA is dominated by deep learning models that can effectively fuse the modalities and capture the temporal dynamics of the data. Some of the notable models are listed below.
Multimodal Transformer (2019)
“Multimodal Transformer for Unaligned Multimodal Language Sequences” addresses two major challenges:
- the data non-alignment due to variable sampling rates for the sequences from each modality and
- The long-range dependencies between elements across modalities as the modalities are not static signals.
At the heart of the model is the directional pairwise crossmodal attention, which attends to interactions between multimodal sequences across distinct time steps and latently adapt streams from one modality to another
the heterogeneities across modalities often increase the difficulty of analyzing human language. For example, the receptors for audio and vision streams may vary with variable receiving frequency, and hence we may not obtain optimal mapping between them. A frowning face may relate to a pessimistically word spoken in the past.
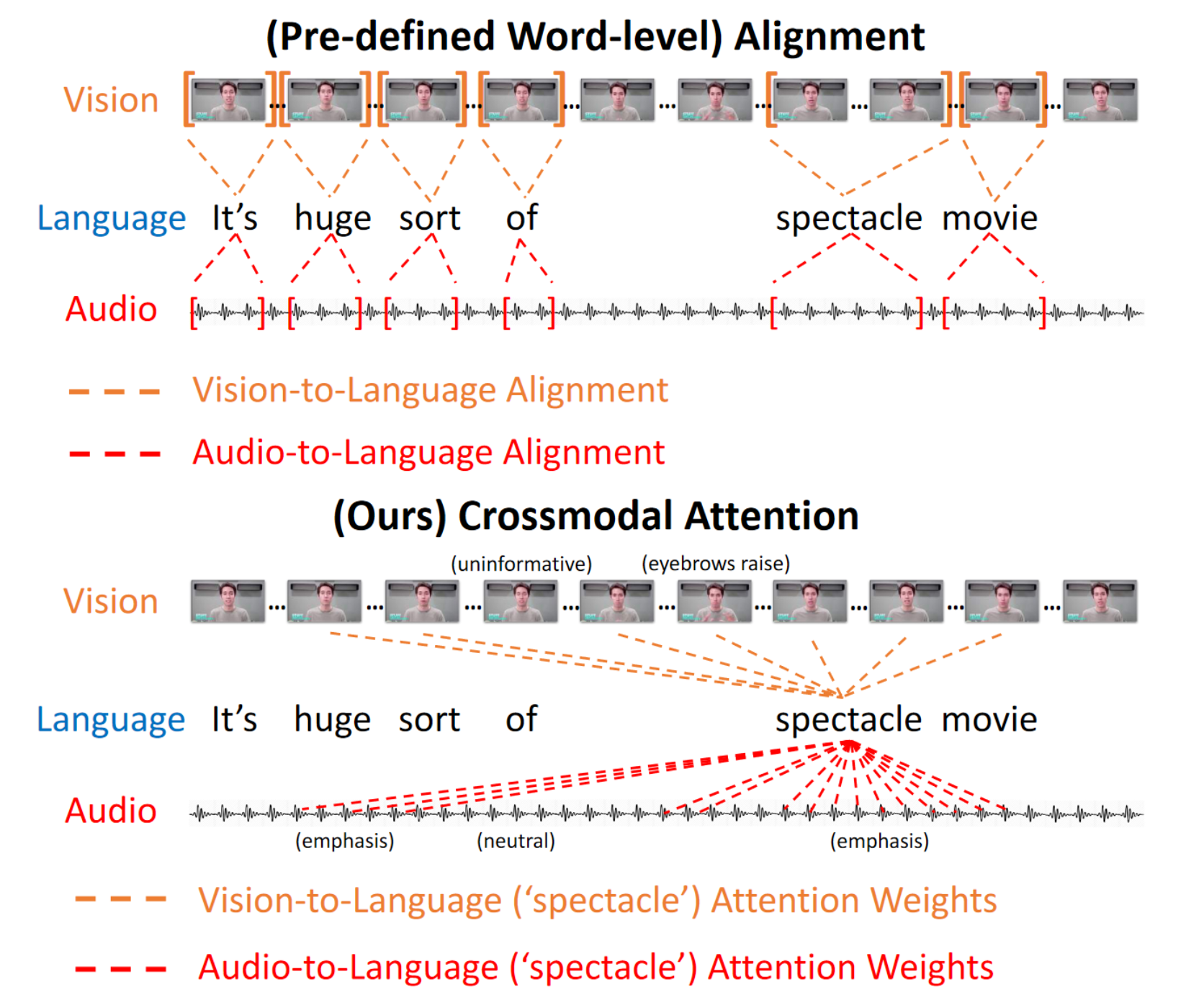
The author says that in empirical qualitative analysis, the crossmodal attention used by MulT is capable of capturing correlated signals across asynchronous modalities.
Model Structure
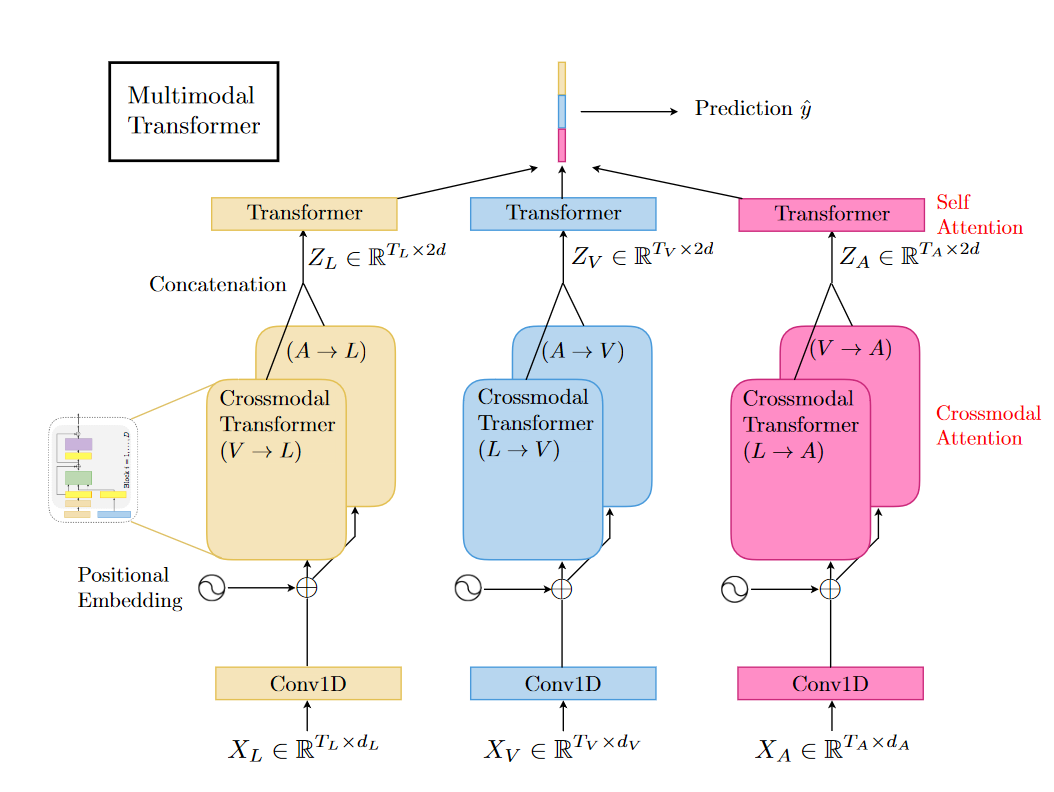
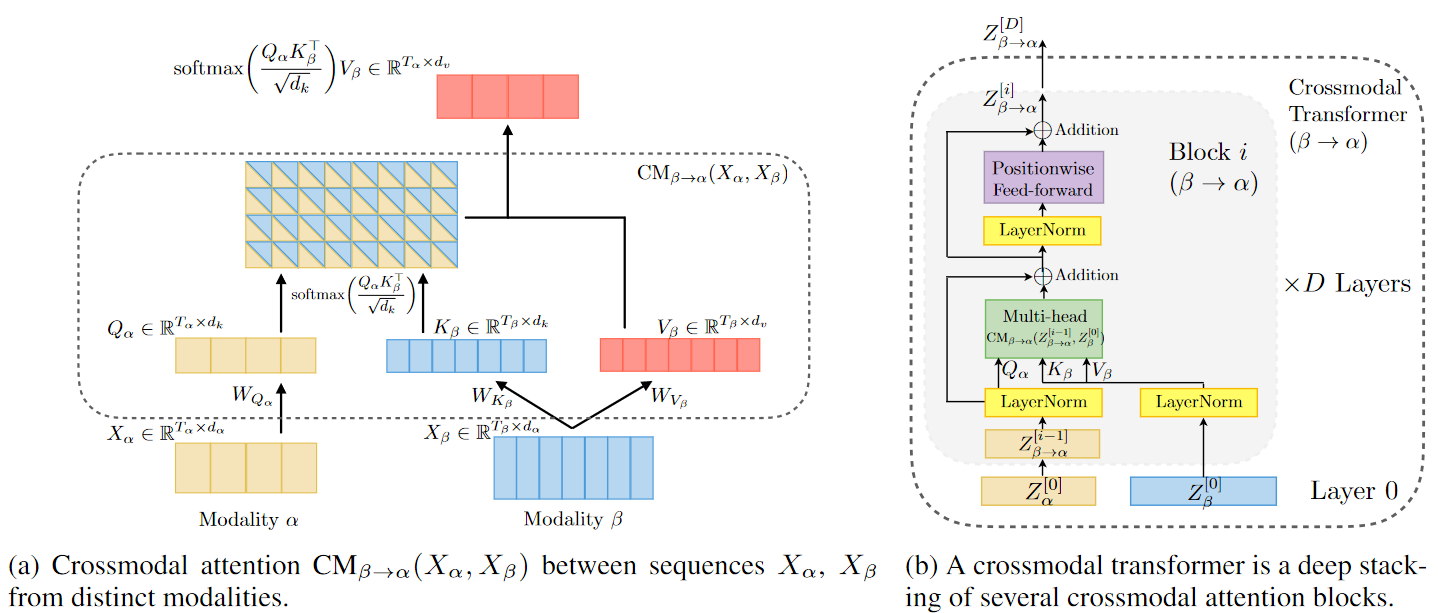
MPLMM (2024)
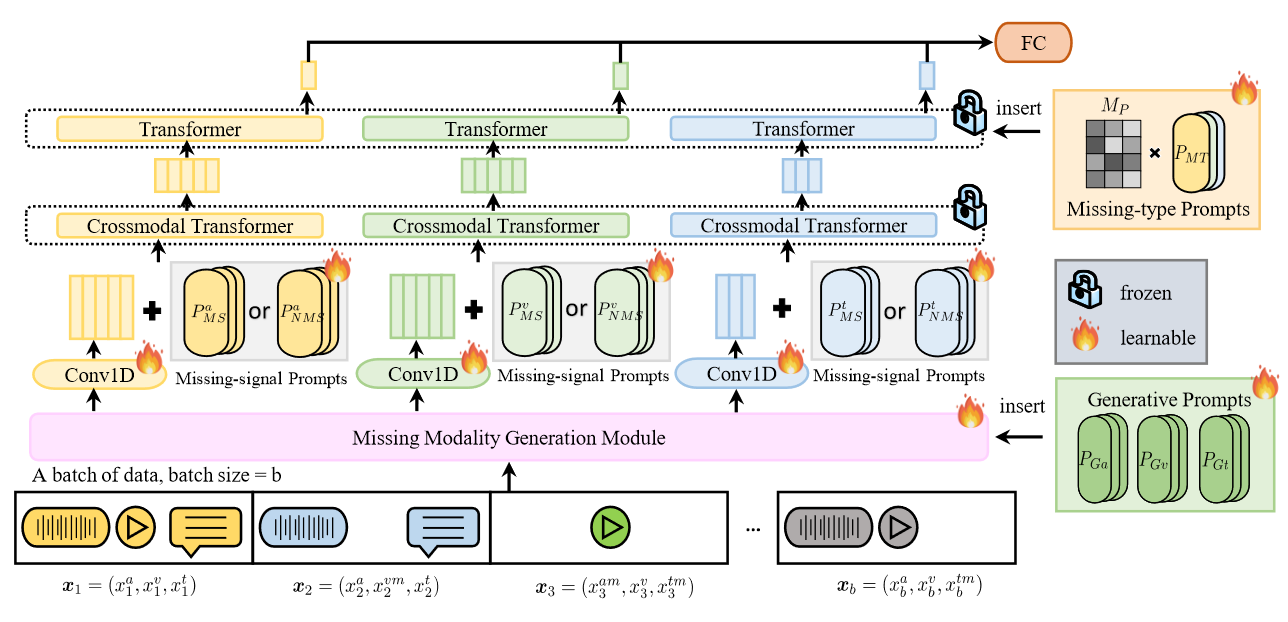
“Multimodal Prompt Learning with Missing Modalities for Sentiment Analysis and Emotion Recognition”. This model is based on the MulT. It find that the presence of missing modalities is a common scenario in real-world applications, existing methods often ignore the missing modalities and only focus on the available ones. Current multimodal models trained on complete data usually fail when tested on incomplete data. This paper proposes a novel multimodal Transformer via prompt learning to tackle the issue of missing modalities. The prosed prompts increase only linearly with the number of modalities.
There are three types of prompts:
- Generative prompts: Help generate missing information.
- Missing-signal prompts: They are desiged to inform the model about the absence of a specific modality.It is modality-specific, it helps the model learns intra-modality relationships.
- missing-type prompts: They are designed to inform the model about the absence of other modalities. It is modality-shared, it helps the model learns inter-modality relationships. With prompt learning, the model can significantly reduce the number of trainable parameters.
Prompt learning
Prompt learning, which refers to the process of designing or generating effective prompts to use a pre-trained model for different types of downstream tasks, has been widely used in various NLP tasks.
This paper’s approach utilizes generative prompts to generate the representation of missing modalities given available modalities which can help further boost the performance of the model.
Model Structure
Problem definition
Given a multimodal dataset D consisting of M = 3 modalities (e.g., audio, video and text), we use $x = (x^a, x^v, x^t)$ to represent a pair of features in D, where $x^a$, $x^v$, $x^t$ represent the features of acoustic, visual and textual modalities respectively. To indicate missing modalities, we use $x^{am}$, $x^{vm}$, $x^{tm}$ to denote which modalities are absent.
Missing Modality Generation Module (MMGM)
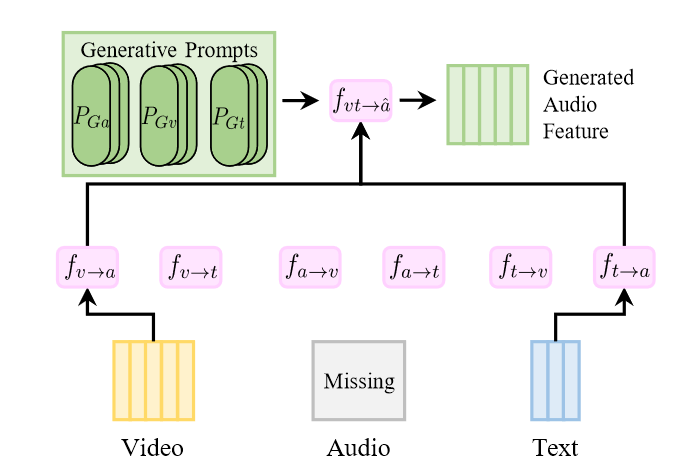
$$ P_G = (P_{Ga}, P_{Gv}, P_{Gt}) $$
Where $P_{Ga}$, $P_{Gv}$, $P_{Gt}$ are the generative prompts for acoustic, visual and textual modalities respectively. $P_G \in R^{3\times d_p\times l_p}$ where $d_p$ is the dimension of the prompts and $l_p$ is the length of the prompts.
In the above figure, given the input $x = (x^{am}, x^v, x^t)$, the MMGM generates the missing audio feature $x^{am}$ by using the available visual and textual features $x^v$ and $x^t$ according to the following equation: $$ \hat{x}^{a} = f_{vt \rightarrow \hat{a}}([ P_{Ga}, f_{v\rightarrow a}(x^v), f_{t\rightarrow a}(x^t)]) $$ where $\hat{x}^{a}$ denotes the representation generated. [. . . ] represents the concatenation operation.
If there are two missing modalities, such as $x = (x^{am}, x^{vm}, x^t)$, the generation process is as follows: $$ \hat{x}^{a} = f_{t \rightarrow \hat{a}}([ P_{Ga}, f_{t\rightarrow a}(x^t)]) $$ $$ \hat{x}^{v} = f_{t \rightarrow \hat{v}}([ P_{Gv}, f_{t\rightarrow v}(x^t)]) $$ After applying the MMGM, we can represent the generated features as $x = (\hat{x}^a, \hat{x}^v, x^t)$.
Missing-signal and Missing-type Prompts
Missing-signal prompts
Missing-signal prompts are designed to inform the corresponding Transformer whether the information for a particular modality is real or generated. For each modality, there are two missing-signal prompts: $P_{MS}$ to denote a modality is missing and $P_{NMS}$ to denote a modality is not missing. For example, after the MMGM and the Conv 1D layer, we obtain features $x = (\hat{x_a}, x^v, x^t)$ where the audio modality is missing originally. We can incorporate the missing-signal prompts as follows:
$$ \begin{align*} \hat{x}^a &= \hat{x}^a + P_{MS}^{a} \newline x^v &= x^v + P_{NMS}^{v} \newline x^t &= x^t + P_{NMS}^{t} \newline \end{align*} $$
After applying missing-signal prompts, the model knows which modalities are generated and which modalities are real, which can help the model make better use of the recovered information. Notably, missing-signal prompts are modality-specific which means that this kind of prompt only considers a specific modality and does not take into account the correlations between the absence of multiple modalities. To address this limitation, they propose missing-type prompts.
Missing-type prompts
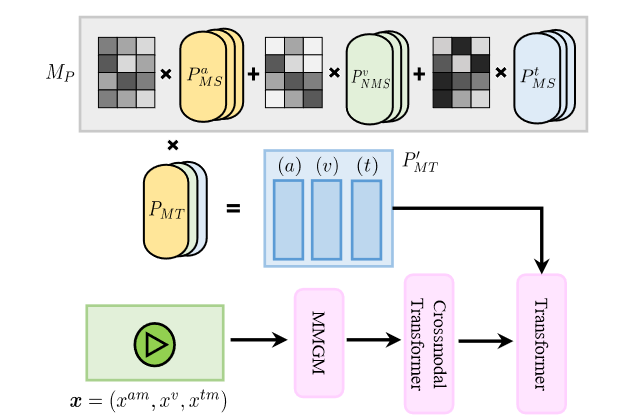
If there are M modalities, there can be a total of $2^M − 1$ different cases of missing modalities. They propose a way to represent these cases in a linear way by introducing a missing-type projection matrix $M_P$ of $x = (x^{am}, x^v, x^{tm})$ as follow:
$$ M_p = M_a \cdot P^a_{MS} + M_v\cdot P^v_{NMS} + M_t\cdot P^t_{MS} $$
where $\cdot$ is the matrix multiplication,$M_a, M_v, M_t \in R^{d_p\times l_p}$ and $M_p \in R^{d_p\times d_p}$. Then, we can get the missing-type prompts $P_{MT}^{′}$ as follows:
$$ P_{MT}^{′} = P_{MT} \cdot M_p $$
Where $P_{MT}$ represents the original missing-type prompts, $P_{MT}^{′}$ represents the projected missing-type prompt. $P_{MT},P_{MT}^{′} \in R^{3\times l_p \times d_p}$
Experiments
To simulate real-world scenarios, They select CMU-MOSEI (Bagher Zadeh et al., 2018) as the high resource dataset while CMU-MOSI (Zadeh et al., 2016), IEMOCAP (Busso et al., 2008) and CH-SIMS (Yu et al., 2020) are selected as the lowresource datasets. They pre-train their the backbone on CMU-MOSEI ( They then freeze the parameters of the backbone and only train several learnable prompts, Conv layers and the output layer) and evaluate the proposed method on the four datasets.
The results can improve the performance of different backbones and it out performs LB, MS, MD, MCTN, MMIN, MPMM on four datasets and the evaluation of the performance on modalities missing rate also have better performance than the other methods.
In the ablation study, they showed with the experiment results:
- Generative prompts learn good representations of the missing modalities and improve the binary accuracy.
- Missing-signal prompts are modality-specific prompts that tell models whether the corresponding modality is missing and help improve the correlation of the model’s predictions with humans.
- Missing-type prompts are shared prompts with inter-modality information, thus helping models learn cross-modal and fine-grained information that improves ACC-7.
They also found that both ACC and F1 score steadily improve as the train set modality missing rate increases, before reaching the highest point when the missing rate η = 70%. This indicates that when the train set missing rate is low, it is difficult for a model to learn very good representations in the MMGM and to learn opportune prompts that can instruct the model well.